Intro:
Web APIs are notoriously hard to secure. As a developer, anytime you expose endpoints/resources to The Internet™ for others to use, it's important to make sure that the people who use those endpoints are who they say they are. We can accomplish this with API Request Signing.
Background knowledge:
This article assumes familiarity with the HTTP protocol, web APIs and a basic understanding of hash functions. I provide a sample implementation in NodeJS/Express. Also, it is important to use HTTPS to protect requests between the client and server, but even if HTTPS is in place you should implement request signing as HTTPS cannot defend against requests from attackers looking to masquerade as real users.
Request Signing Basics
Consider the following system. Tim is our "server", and listens for requests. Alice is our real user, who wants to send a message to Tim. David is the attacker. Alice tries to identify herself to Tim, by sending her name in the request, but if David is able to see her message over the network or otherwise gain access to her "name" field, he can pretend to be her and send false messages to Tim:
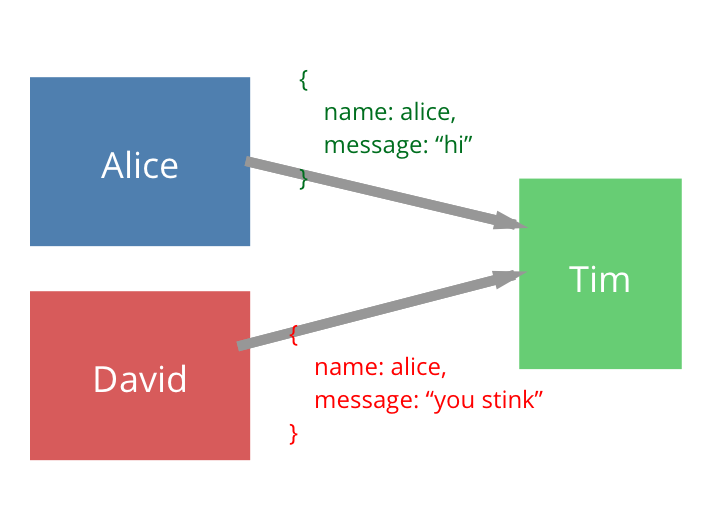
This is a common problem that we face when building web APIs - since users' IDs/usernames are relatively well known, we cannot use these as identifiers. To combat this, we need to implement a MAC (Message Authentication Code), an algorithm which confirms that a given message came from its sender and that the data in the message hasn't been altered in transit.
There are several flavors of MAC algorithms, but the one we'll focus on for now is called HMAC, which stands for Hashed-Based Message Authentication Code.
What is HMAC?
HMAC is a MAC algorithm that depends on a cryptographic hash function. (You may remember from your CS texts that a hash function takes input data and maps it to standardized output data, and that good hash functions produce as few collisions as possible, which means that different input is rarely mapped to the same output.)
Hash functions
In the case of HMAC, we need a hash function that takes a variable-size String input and generates a fixed-size String output. The input cannot be easily decoded using the output, and different inputs must map to different outputs - hash("hi tim") must produce a different result than hash("hi timo").
(If you were able to write a function that satisfies all of the above constraints, please contact me. You'll probably win a Turing Award and I would love a share of the prize money.)
Fortunately, several hash functions (written by some very smart people) already exist. We'll use SHA-256 for this exercise (thanks, NSA). SHA-256 gives us a 256-bit output that is pretty much guaranteed to be unique for any string input. In hexadecimal, each character represents 4 bits, so to for our 256-bit string we'll need a hexadecimal string that is 64 digits in length.
Secrets, Secrets and more Secrets
Now that we've got our hash, we need to assign each user a public key and a private key (secret). The public key will be sent in the request as an identifier. (The private key cannot be exposed in the request, and if an attacker were able to gain a user's public and private keys, they would be able to send requests as that user.) If you've worked with web APIs before, this will sound familiar - most APIs assign an identifier key that matches to a secret.
The diagram below shows this revised state - Alice and David each know their own ID and secret, but not each other's. As the server, Tim is the only one who knows everyone's id and secret.
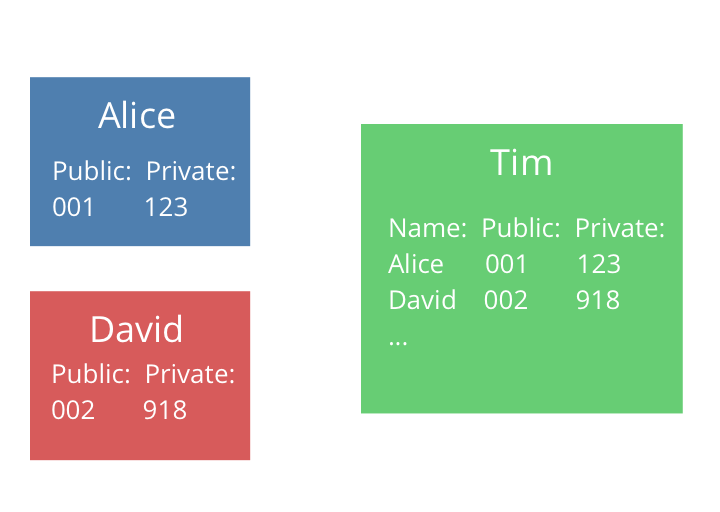
It doesn't really matter how we create these IDs/secrets - they just have to be unique and matchable to each user by the server.
HMAC Signing
Now that we have everything we need, let's sign our request!
First try at a good HMAC
Our first version of the signature will be fairly simple: we'll concatenate the secret key + the message and make a hash of that. We'll attach our signature and the public key to our HTTP request as a header. The server will look for the public key in its database, find the corresponding private key, and calculate the same hash(secret_key + message). If this hash is the same as the signature that we sent in the request, we know 1) the message could have only come from someone with the secret key, and 2) the data in the message hasn't been altered in transit. Wahoo!
Below is our original example, this time with request signing. Alice signs her request with her private key. Tim checks the signature by computing his own hash of the information. Notice how the private key is not passed in the request at all - only the public key is sent, so that Tim can find the corresponding private key. David is angry, because to imitate Alice, he has to 1) successfully guess Alice's private key 2) make his own hash of the message and send it to Tim, which is a lot of work. (In real life, Alice's private key would be much longer than three characters, making the process of guessing the key nearly impossible.)
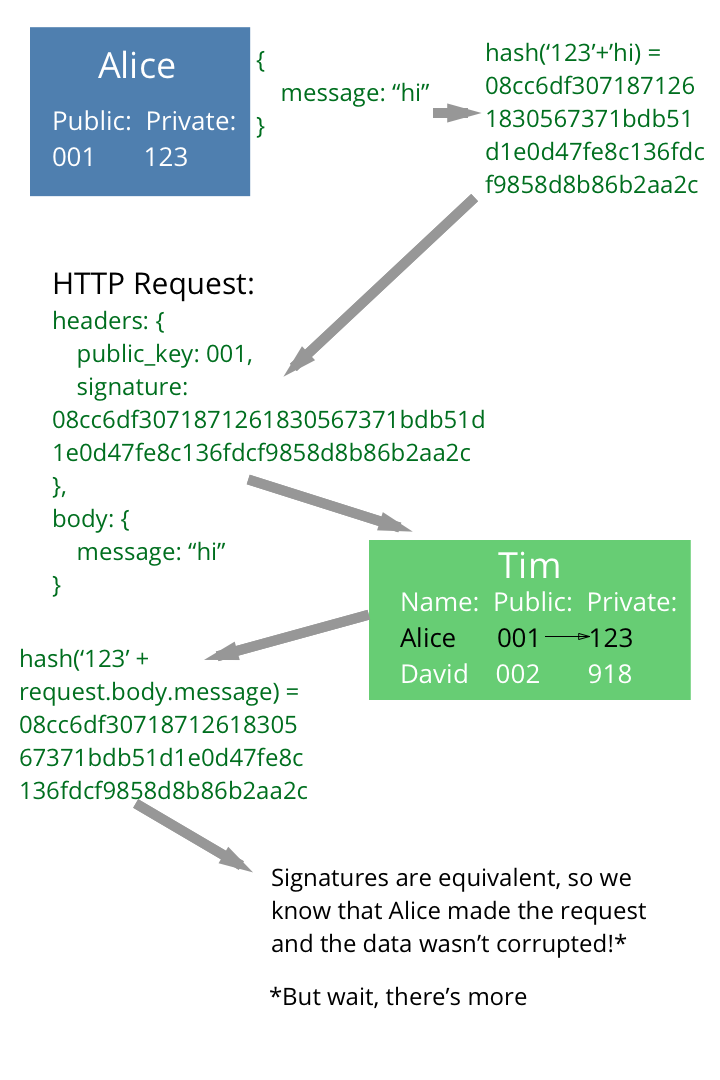
Issues
This is pretty dandy, and solves the initial problem of proving that the message comes from Alice. But we have a small problem. Since the the signature comes from a simple concatenation of the private key + message body, there is an extremely simple way to send a corrupted message: remove stuff from the key and append it to the message. For the example above, suppose the key was '12' and the message was '3hi'. The hash would still be hash('12'+'3hi') = hash('123hi'), giving us the same (valid) signature as our original message! This is no good.
To combat this, the authors of the HMAC algorithm used a pretty nifty trick involving bit math and hashing twice to produce a secure document signature. (I won't go into the proof here, but if you're interested, you can read more about the algorithm in RFC 2104). The final 'secure' algorithm, from the RFC text, is:
1) B is the block size of the algorithm used in bytes. For SHA-256, the block size = 64 bytes.
2) The key must be at most B bytes in length. If the key is less than B bytes, 0s are appended to the key until there are B bytes in the key.
ipad = the byte 0x36 repeated B times
opad = the byte 0x5C repeated B times
key = private key
text = message to be signed (request body)
signature = hash((key XOR opad) + hash((key XOR ipad) + text))
And that's it. Now we've got a signature that pretty much guarantees that Alice is Alice, and is extremely difficult for David to crack.
Implementation
We don't need to implement this ourselves. Most modern languages/frameworks have crypto libraries that have an HMAC implementation already included, or utility functions which you can quickly stitch together: NodeJS, Java, Golang, etc.
Here's a sample signature in NodeJS using the NodeJS crypto library. It's extremely simple.
var hmac = crypto.createHmac('sha256', secret_key);
hmac.update(request.body.message);
var signature = hmac.digest('hex'));
Conclusion
I hope this was a helpful introduction to the HMAC algorithm and API request signing! As I mentioned earlier, request signing is only one of the strategies that you should use to protect APIs/the integrity of messages. You should explore other strategies to help secure your application, especially HTTPS for encryption during transit - production APIs usually use both request signatures and HTTPS to provide a minimum level of security. Feel free to reach out to me at ahoang18 [at] bu.edu with any questions!